区块链中的数学

中国文化重文采，历史故事写的美妙。近代几次寻求文化属性的突破，但时有回潮。西方文化在跨越宗教限制之后，走向了辩证和唯物，追求真理。我们的比特岛看上去是一个美好的世界，但上述可信的交易记账协议里，留了两个数学问题等待我们解决。但这两个数学问题的证明及其复杂，无法用美妙的文字来描述，仅仅是使用这两个原理都不是一般人能够做到的。那我们可以相信这些我们无法理解的科学吗？每一块组成比特岛的砖石，都曾经历百年的风化和打磨，才最终固化为现在的模样。正如科学一样，人类所有持久有效的创造，几乎都和科学有关。而在科学之中，最不容辩驳的就是数学。你看社交网络上大家对一些热点事件七嘴八舌，甚至法庭判案他们都能插上一嘴。但当我抛出一个数学问题时，只闻鸦雀无声。为了向大家解释区块链信任的数学基础，我会用一个章节的篇幅去推演，对于数学不感兴趣的读者可以跳过，只管相信就行。

新的假设

欧几里得大约于公元前300年写成《几何原本》，基于直线，平行线的公理形成了欧式几何。其中的5条公设如下：

从一点向另一点可以引一条直线。
任意线段能无限延伸成一条直线。
给定任意线段，可以以其一个端点作为圆心，该线段作为半径作一个圆。
所有直角都相等。
若两条直线都与第三条直线相交，并且在同一边的内角之和小于两个直角，则这两条直线在这一边必定相交。

几何原本发布以来，数学家们就发现第五公设和前四个公设比较起来，显得文字冗长，而且也不那么显而易见。现在普遍的引申描述为：两条不相交的直线为平行线，而通过直线外一点有且仅有一条直线与该直线平行。有些数学家还注意到欧几里得在《几何原本》一书中直到第29个命题中才用到这第五公设，而且以后再也没有使用。也就是说，在《几何原本》中可以不依靠第五公设而推出前28个命题。因此，一些数学家提出能不能依靠前四个公设来证明第五公设？这就是几何发展史上最著名的，争论了长达两千多年关于“平行线理论”的讨论。由于证明第五公设的问题始终得不到解决，人们逐渐怀疑该公设是否是显然而必要的？

这类放弃或者修改第五公设而产生的几何统称非欧几何。现在有一条直线和直线外的一个点，以“通过该点可以引最少两条平行线”为新公设就是罗氏几何（双曲几何）。以“一条平行线也不能引”为新公设就是黎曼几何（椭圆几何）。当时有不止一位数学家有这样的想法，其中匈牙利数学家鲍耶·亚诺什在研究非欧几何学的过程中遭到了家庭、社会的冷漠对待。他的父亲——数学家鲍耶·法尔卡什认为研究第五公设是耗费精力劳而无功的蠢事，劝他放弃这种研究。但鲍耶·雅诺什坚持为发展新的几何学而辛勤工作。终于在1832年，在他父亲的一本著作里，以附录的形式发表了研究结果。

70多年以后的1905年，另一个人对存在了数百年的经典力学提出了疑问。当时人们认为时间和空间是各自独立的绝对存在，这是自伽利略时代以来就建立的绝对时空观。但描述电磁波的麦克斯韦方程组在伽利略变换下有不协变的问题，加上迈克尔孙-莫雷干涉仪实验，已经有人尝试推导一种空间不变的数学变换。但这个人在开始他的推导之前，引入了一个新的假设：真空中的光速在任何参考系下是恒定不变的。这一光速不变公设，加上惯性参考系的平权性，让爱因斯坦打开了狭义相对论的世界。和非欧几何的诞生一样，这一新理论加入了一个反直觉的公设，得出了诡异的结论，所以在初期只有很少人理解并且认可。但实验结果的支持，让这一理论大获成功，人类从此改变了对世界的认识。

用新公设（公理）开天辟地似乎是不二法门，爱因斯坦尝到了甜头，还想再来第二次！在人们用狭义相对论改造传统物理的协变性时，发现除了万有引力论难以协调以外，其他主要理论都迁移的非常顺利。也就是说在不考虑引力的情形下这种新的物理学具有洛伦兹不变性（狭义相对性原理，又称狭义协变性原理）。为了让任何物理规律都使用与参考系无关的物理量表示出来，整个物理世界跃跃欲试，不就是引力嘛，我们修正他。在大家埋头苦干时，爱因斯坦微微一笑，在一个思想实验中，他打算再一次引入一个新的公设，来迅速解决问题。他想象着，我们习惯认为一个人的体重是引力质量在引力作用下产生的，我们站在地面称体重就可以得到自己的质量。那如果把人放到一个在无重力空间加速飞行的火箭上，人因为惯性产生的“重力”，和引力中的重力，是等效不可区分的。同样不论从哪个参照系测量，物理世界的力学现象也都是等效不可区分的。

这样我们得到了一个新的惯性参照系，就是在引力下自由落体的空间，这里引力和惯性力相抵消。这让真空中羽毛和小球等速落体的现象变得显而易见，但这并没有让问题变得简单。爱因斯坦从1907年开始了长达八年对引力相对性理论的探索，在历经多次弯路和错误之后，他拍拍脑袋，打算引入第三个公设，给这一问题以致命一击。如果说惯性运动是匀速直线运动，那同时也是时空几何上的最短路径（测地线）。在狭义相对论的4维模型里，是闵可夫斯基时空笔直的“世界线”。但现实物理世界不存在全域惯性系，引力无处不在，也就是只有跟随自由落体粒子一起运动的局部惯性系。这导致世界线彼此相互弯曲，这第三个公设就是，引力场是时空弯曲的体现。在解这个时空弯曲的方程时，近百年前打破第五公设的非欧几何起到了至关重要的作用。最终广义相对论诞生，这一理论的怪异程度大大超过了上一次的狭义相对论。一下引入两个超前的公设，就好像出拳用力过猛，即使积累了一定名声的爱因斯坦也难以驾驭。直到1915年通过广义相对论证明了水星轨道的近日点反常进动现象，和日食光线在太阳引力场中的偏折现象（预测角度是传统理论预测值的2倍），新理论才被广泛接受。

世界上经历了几代人的锤炼，最终留下来的创世公理（公设）并不多。如果当时有知乎一定会有人问，10年间提出3个全新公设是怎样的体验。在新理论下物理学蓬勃发展，构建在那些久经锤炼的公理支柱上，人类生产力迎来腾飞。路德维希·维特根斯坦也早早下了定论：凡能够说的，都能够说清楚；凡不能谈论的，就应该保持沉默。从此除了在现有框架下做拓展外，很多学者一定不时会拿起小榔头，在这些公设支柱上敲敲打打，看看有没有什么东西松动了掉下来。科学大厦越建越高，而他的根基也越发牢固，希尔伯特提出的23个世纪问题中的第二个，就是公理系统内的命题彼此是否相容无矛盾。在1930年哥德尔不完备定理（Gödel's incompleteness theorems）证明之后，粉碎了希尔伯特的梦想，也粉碎了理论学家的小榔头。旷世骇俗的新公设，也许只有等到我们的观测能力大幅提升，有了全新的实验发现之后吧。

走出接近完美的数学和物理，还有什么算是能够说清楚的呢？罗纳德·费希尔在他1935年的著作实验设计（The Design of Experiments）一书中，举了一个女士品茶的例子。那是20世纪20年代后期，在英国剑桥一个夏日的午后。一群大学的绅士和他们的夫人们，还有来访者，正围坐在户外的桌旁，享用着下午茶。在品茶过程中，一位女士坚称：把茶加进奶里，或把奶加进茶里，不同的做法，会使茶的味道品起来不同。在场的一帮科学精英们，对这位女士的“胡言乱语”嗤之以鼻。这怎么可能呢？他们不能想象，仅仅因为加茶加奶的先后顺序不同，茶就会发生不同的化学反应。然而，在座的一个身材矮小、戴着厚眼镜、下巴上蓄着短尖髯开始变灰的先生，却不这么看，他对这个问题很感兴趣。他兴奋地说道：“让我们来检验这个命题吧！” 并开始策划一个实验。在实验中，坚持茶有不同味道的那位女士被奉上一连串已经调制好的茶，其中，有的是先加茶后加奶制成的，有的则是先加奶后加茶制成的。

有的读者可能觉得，这和传统的物理化学实验并没有不同，只要确定每次预言正确，就可以得出结论。但要知道，参与实验的是人，人的行为并不像物理世界那样一成不变。这位女士即使瞎猜，在第一杯也有50%的概率猜对，到第二杯连续猜对的概率为25%，第三杯12.5%...以此类推。那到底要猜对几杯，我们才敢断定这位女士真的可以品出不同顺序调制的奶茶来？这是一个不那么容易说清楚的事，是一个开放性问题而不是简单的确定性假设。后来这种不确定性也写进了以严谨著称的物理学，在量子力学里，上帝玩起了筛子。

今天我们不打算敲打那些恒久的公设，我们只想问这么一个问题，如果去掉所有信息系统中的中心管理节点，还能否继续维持这个系统的运作？如果能运行的话，执行效率如何？这个问题的答案，就是我们今天要讨论的去中心化高效分布式系统。区块链作为最早一块拼图，让我们暂且沿用他的名字，将这套体系称为狭义区块链。去中心的不光是信息系统，其实我们看整个物理世界，就是由公式和计算组成的。这么多的粒子，在相同的时空里，完全遵守统一的规律，一刻不差。如果要模拟这样的世界，那需要的计算量人类恐怕永远无法完成。这么一个近乎完美的世界，是不是也算一种去中心化高效分布式系统的实例？目前这套狭义区块链还在发展和证明自己，距离高效还差很远。期间和人类社会金融系统的摩擦不断，掀起的融资狂潮和价格崩盘一样频繁。为了修正这个问题，已经有很多的努力，而我们打算引入一个非常危险的假设：区块链账本的余额可以为负。这一改变带来的一连串问题，会大大超过本书的范围，所以我们暂且称之为广义的区块链模型，留待后续去挖掘其内涵。但设想一下暗物质的存在，宇宙的诞生可能就是因为借了一点点能量，带来的一次非平衡波动。

费马大定理

这是一个困扰数学界300多年的问题，由“业余数学家”费马提出。他出生在17世纪初的法国，职业生涯本和数学无关，是图卢兹议院的顾问，就是一名政府文官。当时正好在红衣主教黎塞留(Richelieu)晋升为法国首相3年后，政府机构里充斥着阴谋和诡计。费马显然对这些人世间的问题不感兴趣，他有效的履行自己分内的职责，不站边，也尽量不把人们的注意力引向自己。在避开了议会混战的同时，将自己余下的精力都奉献给了数学，被埃里克·贝尔(Eric Temple Bell)称为“业余数学家之王”。但朱利安·库利奇(Julian Coolidge)不这么认为，在写作《业余大数学家的数学》一书时将其排除在外，因为“他那么杰出，他应该算作专业数学家”。要知道当时数学还在从欧洲中世纪的黑暗中逐渐恢复，不是很受重视的学科。

巴黎数学家们有个守口如瓶的奇怪传统，这是从16世纪cossists沿袭下来的。cossists是指精通各种计算的专家，受雇于商人和实业家，以解决复杂的会计问题。所以出于利益考虑，这个时代的专业解题者都努力创造他们自己的聪明方法来进行计算，并且尽可能的保密。唯一例外的是梅森尼神父，他试图鼓励数学家们相互交换自己的思想，以相互促进。他作为唯一与费马定期接触的数学家，一直鼓励费马将他的研究公布。但费马不为所动，公开发表和被人们认可对他来说没有任何意义，他以创造和发现新的未被他人触及的定理为乐。他甚至在与友人的通信里不时挑逗，描述他最新的定理但不提供任何相应的证明。这种习惯让人咬牙切齿，但费马的贡献如此之大，大家前赴后继的追求他定理的证明。甚至在普遍认为是微积分发明者牛顿的一个注记里也写到，他是在“费马先生的画切线法”基础上发展了他的微积分。

费马留下的遗产被后人反复研习，他那些刻意隐藏证明的定理，终于被后人一一验证。这一次激发他灵感的是亚历山大的巨著《算数》，其中求等式有理数解的丢番图方程引起了他的注意。在《算术》第二卷中，描述了毕达哥拉斯定理和毕达哥拉斯三元组。这个定理其实就是勾股定理，古代中国早在公元前一千多年就已有论述。毕达哥拉斯对勾股定理的证明方法和三国时期的赵爽一样。但费马关心的是这个问题的扩展，既然二次方等式能够成立，那么三次方，以及更高次幂的勾股方程能有整数解吗？ $x^2 + y^2 = z^2$ $x^3 + y^3 = z^3$ $x^n + y^n = z^n$

挑逗的费马在研究完这个问题以后，老毛病又犯了，在书的页边处记下了他的结论：

不可能将一个立方数写成两个立方数之和，或者将一个4次幂写成两个4次幂之和，或者总的来说，不可能将一个高于2次的幂写成两个同样次幂的和。我有一个对这个命题的十分美妙的证明，这里空白太小，写不下。

在费马恶作剧般的其他定理早被验证完毕的百年后，唯独这一个看似非常简单明了的定理，无人能证。从此我们将这个问题称为费马大定理。而这一切看上去都只是中学数学而已，也确实对4次幂的证明在费马手稿中透露了些许线索，很快得征。但为了证明3次幂，我们已等了百年。直到18世纪的天才欧拉，通过引入虚数的概念，再结合4次幂类似的套路，完成了证明。而这也只是漫漫长路上的一小步，人们不断攻破各种非质数的情况，但余下需要证明的数量还是无穷。一直等到新世纪的数学进入抽象，我们才迎来曙光。这里第一个难啃的概念叫椭圆函数。

椭圆函数与丢番图

科学本身有一种很友善的性质：问题可以被清晰的描述，而结论可以相对容易的验证。费马大定理是否定式定理，所以穷举验证起来很费力。但我们换一个有解且容易验证的丢番图谜题，号称史上最贱的数学题为例，来告诉大家，再难以理解的数学，其可靠性是相对容易验证的。这道题及其解答来源于Quora问答网站，并由知乎网友授权翻译。

题目是如下这张图片，第一眼看到的时候，你绝对会以为这又是什么脑筋急转弯的趣味问题。在我们开始枯燥的数学之前提醒读者，只要你看明白了问题，而对于证明过程不敢兴趣，那可以直接跳到结尾去验证我们的结论。当然想挑战这个趣味“脑筋急转弯”的朋友也可以跟着我们一步步的进行数学求解。这就是科学善解人意的地方。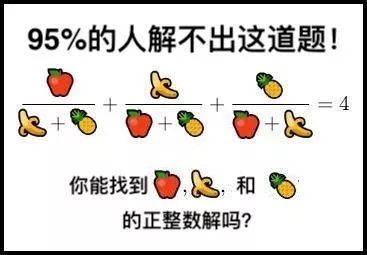

用a,b,c替换苹果，香蕉和菠萝，我们可以很快得到题目的数学描述，就是解下面的3元方程：
$\frac{a}{b+c} + \frac{b}{a+c} + \frac{c}{a+b} =4$

等式两边相乘去分母后可以发现是三元三次方程，这里似乎已经有些不详的预感：
$a^3 + b^3 + c^3 - 3(a^2b + ab^2 + a^2c + ac^2 + b^2c + bc^2)- 5abc = 0$

多项式方程很容易找到某个特解，比如说， a=−1 ，b=1, c=0。但这些解还要带回原方程以确认分母不为零。
这意味着我们的立体方程（3维）实际上是个椭圆曲线
但这里不是大家熟悉的圆锥曲线中的椭圆，而是复域上亏格为1的光滑射影曲线，好像一个甜甜圈。
对于特征不等于2的域，它的仿射方程可以写成：
$y^2=x^3+ax^2+bx+c$

这个复数域上亏格为1的黎曼面，被Mordell证明其有理点是有限生成交换群（有限域），这是著名的BSD猜想（世界7大难题）的前提条件，所以我们就不在这里费劲的解释细节了。大家唯一需要紧记的是，方程整数解也组成一个有限域，通过其中任意一个解，可以推算出其他的整数解。所以现在我们需要把原方程给椭圆曲线化，变成所谓魏尔斯特拉斯（Weierstrass）形式。这是一个长得像这样的等式：
$y^2=x^3+ax+b$

即使你不知道如何完成变换，验证它是很容易的，或者说至少是机械的。对于我们而言，需要的变换由令人生畏的公式导出。
$x=\frac{-28(a+b+2c)}{6a+6b-c}$ $y=\frac{364(a-b)}{6a+6b-c}$

得到的这个方程尽管看起来和原方程长得不怎么像，但确是如假包换的可靠模型
$y^2=x^3+109x^2+224x$

在实数域的坐标上它长成这样，一条有着两个实部的经典椭圆曲线，右边的“鱼尾”连续延伸至正负无穷。左边的封闭椭圆曲线将成为解决问题的契机。：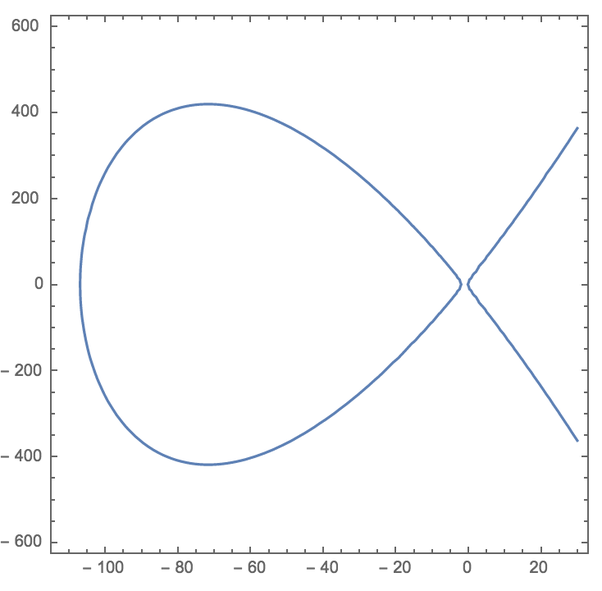

我们略过一些内容，直接找到一个很好的有理数点x=−100, y=260，通过下面的等式还原对应的a,b,c
$a=\frac{56-x+y}{56-14x}$ $b=\frac{56-x-y}{56-14x}$ $c=\frac{-28-6x}{28-7x}$

得到的a,b,c乘以公分母14，就变形为 a=4,b=−1,c=11。带入原方程，验证确实等式结果为4。只可惜这个解有一个负数，不满足题目的条件。但至少我们验证了上述的变换是成立的。
$\frac{4}{-1+11}-\frac{1}{4+11}+\frac{11}{4-1} = 4$

现在一旦你在椭圆曲线上找到了有理数点，就可以利用弦切技巧进行加法，生成其它的有理数点（有理数的加法是封闭的，有理数加有理数还是有理数）。这种加法需要用到近世代数中阿贝尔群，是一种满足满足二元运算定律的代数结构，我们姑且叫做椭圆曲线加法。经过相同点做切线，不同点做连线，取交点的垂足镜像，形成“有限加法循环群”，就能逐一找到方程的解。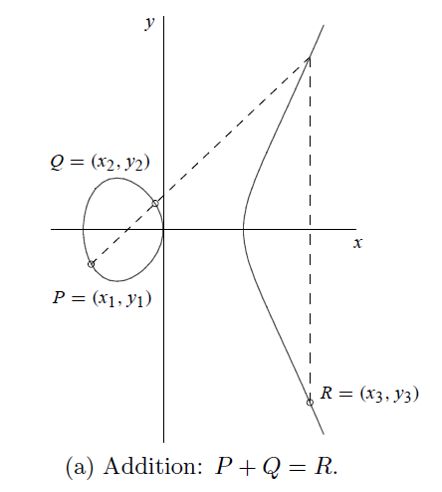

一开始，我们可以通过作P点(x=−100, y=260)的切线，找到它和曲线再次相交的点，以此增加P点的值。结果开始变得有点吓人
$P+P=2P=( \frac{8836}{25},\frac{-950716}{125})$

这个新的点也对应一组a，b，c的值 (a,b,c)=(9499,−8784,5165)，很遗憾这组解也有负数。

我们继续计算3P=2P+P，计算4P，5P等等等等，直到我们计算到9P，对应的a, b, c的值就非常恐怖了

a=154476802108746166441951315019919837485664325669565431700026634898253202035277999,  
b=36875131794129999827197811565225474825492979968971970996283137471637224634055579,  
c=4373612677928697257861252602371390152816537558161613618621437993378423467772036

终于这里没有负数，而且经过很简单的计算机验证，确实满足求和为4的方程。这就是这道题的答案，一个80位数的答案，显然是不可能通过瞎蒙或者暴力手段去破解的。你不一定看得懂过程，但是可以简单的验证答案，那么就姑且相信科学是对的吧。

诡计或真理

椭圆函数只是费马大定理破解之路的一个途经点，最终在成千上万的途经点里，要保证不迷路，不算错，没有漏洞，可以说是人类史上最大的挑战。为此法国科学院设立了一系列的奖项，包括金质奖章和3000法郎奖金，以奖励能最终揭开费马大定理神秘面纱的数学家。在奖金和声望的诱惑下，诡计和真理在搏斗。巴黎的沙龙里充斥着关于某某正在采用某种策略尝试解题，以及距离宣布结果还有多久等等传闻。就好像区块链最火爆的2017、2018两年，业界大量的企业家和研究员投身该领域，每天都有人宣布自己发明了某种更加高效的共识算法，或者上线了某个区块链项目，以及某某加密币涨势喜人等等。每周都有大量区块链聚会，每月有小型发布会，每年在全球各地争相邀请富有声望的专家和明星项目同台论道。那时法国数学界也一样，在1847年3月1日，科学院举行了极富戏剧性的会议。

首先上台的是曾经证明费马大定理在n=7时成立的数学家加布里尔·拉梅(Gabriel Lamé)，面对台下当时最卓越的数学家们，他宣布自己差不多已经证明费马大定理了。虽然当前证明还不完整，但是他概述了他的方法，并预言几星期后发表。全体听众都愣住了，但是拉梅一离开讲台，另外一位巴黎最优秀的数学家奥古斯丁·路易斯·柯西(Augustin Louis Cauchy)也请求发言。他宣布自己在用拉梅类似的方法进行研究，并且很快也将完成。柯西和拉梅都意识到时间的重要性，谁先提交完整的证明，谁将获得一切，而晚来的那个人，将一无所获。仅仅过去3个星期，双方各自发布声明，宣传已将完整证明盖章封印，存放在科学院内。

有了封印的时间作证，整个4月，柯西和拉梅都在不间断的透露这个证明的细节，但却又保持着一份神秘，亦或是某种不安。要知道费马的这个谜题如此简洁，但证明却如此困难，能够理解和跟上这两位领跑者的人并不多。在数学的巅峰是孤独，不像区块链将简单的交易交给全世界去论证，能够胜任前沿数学校验的人屈指可数。这一次站出来的是德国数学家恩斯特·库默尔(Ernst Kummer)，这位最高级的数论家对法国科学院发生的事件一清二楚。从柯西和拉梅透露出的少量细节里，看出这两个人在走向同一条逻辑的死胡同。两个人的证明里依赖“唯一因子分解”这个性质，对于给定任意数，都只有一种可能的质数因子组合。因为质数本身无法继续拆分，所以当因子分解到最后，剩下全都是质数的时候，显然具有唯一性。这一性质如此明显，历年来并未受到质疑。但是前面提到，在解决费马大定理n=3的情况时，欧拉引入了虚数。

以12为例，在实数域上，可以分解为2 x 2 x 3。但在虚数域里，还可以分解为如下形式： $12 = (1+ \sqrt{-11}) \times (1-\sqrt{-11})$ 虚数的引入，使得因子分解不唯一。这一瑕疵在小于31的质数可以避免，但是在例如n=37,59,67这种非规则质数下，无法完成证明，所以费马大定理没有完全解决。库默尔的发现对拉梅是极大的打击，他也意识到如果将自己的工作更为公开一些，或许就会更早发现这样的错误。但柯西拒绝失败，他认为自己的方法对唯一因子分解依赖较少，还可以挽救。随后几个星期他还在坚持研究和发表。但夏季接近尾声，秋风将摇曳的树叶吹落，柯西也变得安静了。那两份盖章封印的证明再也无需打开，柯西在1857年撰写了这场科学院关于费马大定理奖项的最终报告，通往证明的道路仍然停留在库默尔指出的那个问题下。很多人觉得在当下数学知识框架内，费马大定理恐怕无法解决。这是数学史上暗淡的一页，委员们建议撤销对费马大定理的竞赛，而将奖励颁给库默尔先生。

也许只有在数学的领域，进攻并不总是获得奖励的那一方。每一扇数学大门的背后，都有一代代坚韧的守门人把守。他们的贡献值得获得最高荣誉的奖励。在他们严谨而睿智的审视下，数学大厦越建越高。经过了椭圆函数与模形式，经过了谷山－志村定理，在20世纪数学的虚拟世界里，英国数学家安德鲁·怀尔斯(Andrew John Wiles)通过7年的孤独探索，最终宣布找到了那个困扰300多年的证明。这份200页的证明摆在最后一代守门人面前。考虑到这个证明的重要性，这次的审稿人不是通常的2~3位，而是6位。其中第三章由尼克·凯兹(Nicholas Michael Katz)负责。考虑到这一章节有70页长，占全部证明的2/3，所以在他坚持下，邀请到当时也在巴黎的吕克·伊卢齐(Luc Illusie)作为合作审稿人。两人日复一日，逐行检验着论文。通过和作者怀尔斯的不断交流互动，他们解决了一个又一个描述不明确的小毛病，最后在又一个“小毛病”上停了下来。但这一次看来遇到了真正的麻烦，怀尔斯不得不再一次把自己关起来，重新上路寻找修复的方法。这时外界充满了各种猜想，人们担心1847年夏天的那个暗夜再次降临。

所幸怀尔斯7年的积累没有白费，最后的灵感闪现，让他如释重负。在全世界的目光下，数学巅峰的钥匙失而复得，其中的感动难以言表。那篇修正后的论文缩减到130页，手稿名为《模椭圆曲线和费马大定理》，是历史上核查最彻底的数学稿件。数学大厦就这样在天才的进攻者和睿智守门人的合作下，提高了一层。复建在数学大厦上的物理，工程等等应用学科依然牢固。这种牢固，其实也脆弱，因为最前沿的科学，依赖的不过那几位守门人。一方面依赖他们的技能，另一方面依赖他们的品德。不论技能还是品德，都不是天生的，可以说这样的守门人，必须由社会环境培养而来。伟大的教育，使社会追求真理，顶尖的名校，让大家相信真理。社会道德的堕落最多让生活徒增艰辛，而知识道德的堕落，让科技大厦崩塌。

我们身边有很多能言会道的意见领袖，针砭时弊的秒文精彩叫绝。但当你和数学家说话的时候，会觉得别扭。每次被提问，他们都会先停顿一下，停顿的长度让你觉得他们睡着了。当他们再开始说话时，听起来却都井井有条。因为在面对每一个问题时，数学家都会在庞大的逻辑空间里反复求证，最后才得出一个他们认为最精确的文字表达。显然在使用文字和数学符号之间，他们觉得后者更加严谨。还是那个苏格兰黑羊的经典笑话，我们稍加改编：

有一个公知，一个物理学家、一个天文学家和数学家走在苏格兰高原上，碰巧看到一只黑色的羊。“啊” 天文学家说道：“原来苏格兰的羊是黑色的。” 物理学家不满意，“得了吧，仅凭一次观察你可不能这么说。你只能说在苏格兰有一只黑色的羊” 。“也不对” 数学家补充道，“只能说在这一时刻，这只羊，从我们观察的角度看过去，有一侧表面上是黑色的。” 这时公知咳了一下说到：“看来现在学生们的学习压力太大，学校招生考试也越来越难，尽出一些刁钻的题目。家长都不会，搞得同学们各个钻进了牛角尖。”

众人走过以后，艾德蒙·兰道的灵魂按奈不住，喃喃自语道，你们怎么知道那个黑色的东西，真的是一只羊？原来很久以前有人问埃米·诺特(Emmy Noether)的同事艾德蒙·兰道(Edmund Landau)，诺特是否真的是一个伟大的女数学家？他回答说：“我可以作证她是一个伟大的数学家，但是对她是一个女人这一点，我不能发誓。”

现代密码学

从二战时期德国的英格玛密码机开始，现代加密手段不断加强，在通讯和计算机领域得到广泛应用。不管方法如何，设计方向都是寻找一种单向的计算，加密非常容易，而解密的逆运算格外艰难。只有在掌握了某种关键信息的时候，才能快速解读。我们用两个大质数相乘就可以简单构造这样一种系统：

p=12026655772210679470465581609002525329245773732132014742758935511187863487919026457076252932048619706498126046597130520643092209728783224795661331197604583
q=8002511426596424351829267099531651390448054153452321185350746845306277585856673898048740413439442356860630765545600353049345324913056448174487017235828857
p*q = N

这里已知p和q，计算N非常容易，但已知N，要做质因素分解则相对困难。而给你N和其中一个因子p，你计算q又变得非常容易。这就是我们要的性质，经过更加强化的构造，就是RSA密码系统的基础。该类方法我们统称为非对称加密，在通信前，需要双方在各自系统里生成自己的私钥和公钥，公钥公开给对方，用来传信，私钥自己保留，用来读信。整个环节除了质数乘法外，显然还依赖一种随机数生成规则，正是这个规则埋下了软件后门的隐患。

RSA Security是由RSA算法的发明者Ron Rivest, Adi Shamir和Len Adleman在1982年创立，作为互联网通讯的基础运行在大量计算机上。后来该公司在2006年以21亿美元的价格被EMC公司收购。但据NSA前通讯员斯诺登所提供的机密文件显示，NSA跟RSA达成了一份价值1000万美元的合同，前者通过在后者的加密软件中植入一个缺陷公式，为自己留了一道“后门”。据悉RSA存有缺陷公式的软件叫做Bsafe，而该缺陷公式的名字为Dual Elliptic Curve，函数方法是DUAL_EC_DRBG，意为双椭圆曲线确定性随机数发生器。没错，这里的椭圆函数，就是史上最贱数学题里的椭圆函数，也是费马大定理里涉及的椭圆函数，更是后来区块链加密币里常用的椭圆曲线。它由NSA开发而出，自2004年起就开始在RSA的软件中使用这一缺陷公式，并受到大量密码学家们的批评。看到这里相信大家都忍不住呼唤库默尔、凯兹那些正直的数学守门人。不论听上去多美妙的理论，在魔鬼的诡计里，都是通往地狱的暗道。索性10多年后NSA带着悔恨放弃了这个后门。

但密码学从不停步，椭圆曲线本是连续的，并不适合用于加密，所以必须把椭圆曲线变成离散的点。我们把椭圆曲线定义在有限域上，先给出一个有限域Fp。Fp中有p（p为质数）个元素0,1,2,…, p-2,p-1，其加减乘除的定义是对P取模，也就是结果除以P取余数，以控制数值在有限域内。Fp域内运算同样满足交换律、结合律、分配律。基于该有限域生成椭圆曲线E(Fp(a,b))，p为质数，x,y∈[0,p-1]，函数表述为： $y^2 \equiv x^3 + ax + b (\mod p)$ 选择两个满足下列约束条件的小于p的非负整数a、b就可以完成构造 $4a^3+27b^2 \neq 0(\mod p)$ 考虑Q=kG ，其中Q、G为椭圆曲线Ep(a,b)上的点，n为G的阶（nG=O∞ ），k为小于n的整数。有限域中的加法和乘法是有特殊规定的，根据加法法则，给定k和G 计算Q很容易。但反过来给定Q和G，求k就非常困难，因为加法取mod循环n次时，对应的减法逆推可能要2^n。而且实际使用中的椭圆曲线p取得相当大，n也相当大，要把n个解点逐一算出来列成上表是不可能的。这就是椭圆曲线加密算法的数学依据。比特币系统选用的secp256k1中k（k<n）为私有密钥（privte key），Q为公开密钥（public key)，其他参数如下：

p = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
- = 2^256 − 2^32 − 2^9 − 2^8 − 2^7 − 2^6 − 2^4 − 1
a = 0， b = 7
G =04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
n = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
h = 01

“透明保险箱签名记账余额开放协议”里无法篡改的签名，就是基于比特币椭圆曲线加密算法 ECC (Elliptic curve cryptography)的一种椭圆曲线数字签名(ECDSA)。他对于数字的单向放大能力，造就了签名算法容易生成，容易验证，但是难以破解的特性。他和量子时代的OTS单次抗量子（匿名与隐私章节会单独介绍）签名一样，成为了区块链信任的基石，被用到不同的项目里。需要提醒的是，上述我们自己创造的协议，加上区块链的数学工具，仍然和真正的比特币协议有些许差异。我们不打算在这里解释具体的比特币交易协议是什么样的，但是通过我们对数学的信任，对交易的推导，相信大部分读者已经可以理解比特币颠覆性的运作机理。“信任源于认知”，有时候守门人也是可信的，那对于没有看过比特币源代码的人，我们只需要相信基本的经济规律。世界上这么多聪明人在没有串通的情况下，一致认同且投入大量的精力物力在比特币之中，他们不是为了骗你的那一点钱，这样不经济。“对于社会群体的信任源于经济学原理”，所以当比特币和区块链已经是社会群体现象时，对他的顾虑可以打消了。

拜占庭分布式系统

如果说密码学是区块链的左腿，那分布式系统就是区块链的右腿。这个计算机领域的热门话题包含了寻址协议，网络通信，传输协议，一致性校验等等问题，复杂度并不逊与密码学。其中皇冠上的明珠就是拜占庭容错的分布式，这个拜占庭问题源于一个流传久远的段子。始作俑者是莱斯利·兰伯特（Leslie Lamport），他是微软研究院的首席研究员，曾获得2013年图灵奖——计算机界的诺贝尔奖。这家伙觉得故事让问题变得受欢迎，因此他在提出观点和问题时常用故事背景吸引眼球，拜占庭将军的故事就是兰伯特在研究分布式系统容错性的时候编出的一个故事，原文如下：

We imagine that several divisions of the Byzantine army are camped outside an enemy city, each division commanded by its own general. The generals can communicate with one another only by messenger. After observing the enemy, they must decide upon a common plan of action. However, some of the generals may be traitors, trying to prevent the loyal generals from reaching agreement.

假设拜占庭帝国的几支军队在敌人的城池外扎营，每支军队听命于自己的将军，这些将军之间只能通过信使传递消息。在对敌军进行侦察后，将军们必须制订一份共同行动计划。但是，有些将军可能是叛徒，这些叛徒会阻碍那些忠诚的将军达成共识。

为了简化问题，将各支军队的行动策略限定为进攻或撤离两种。因为部分军队进攻部分军队撤离可能会造成灾难性后果，因此各位将军必须通过投票来达成一致策略，即所有军队一起进攻或所有军队一起撤离。系统的问题在于，将军里可能有叛徒，他不仅会发送错误信息，而且可能选择性的两面派。比如对支持进攻的说他支持撤退，又对支持撤退的说他支持进攻。比特币的信任和公平机制，可以证明是满足拜占庭容错 (Byzantine fault tolerance) 的。首先信息有数字签名不会被伪造，而且信息广播对所有人透明，一旦认证后不可篡改。所以只要叛徒将军的比例不超过50%，好将军还是可以达成一致的行动，并作出正确的选择。如果叛徒超过50%且相互串通，他们可以对所有好的将军说支持进攻，但其实内部达成不进攻的决议。这样以不到一半的兵力盲目进攻，会导致溃败。

但这里面临很多假设，通讯可靠性的假设，延迟假设，消息记录的假设，不同情况下会得出完全不同的共识机制。最轻的假设是问题节点只有一种报错，就是失联，如果联通，消息内容便是可靠的。那只要在网络层维护一个节点通讯录，略过超时无响应的节点，其余在线节点可以非常容易的达成数据一致。这就是中心化系统里最常见的分布式架构，解决的问题也仅限在节点宕机和部分网络崩溃的情况。假设稍微放开一点，节点间存在假消息，而且节点间的广播同步不做历史记录。你会发现慢慢的，诬陷的温床开始滋生。发送者C可以对A，B两个节点发送两个版本的消息。AB收到以后彼此广播同步会发现矛盾，A会觉得B是叛徒，而B觉得A是叛徒。因为C的两面派行为没有证据记录，这就造成了完美犯罪。现在有些共识机制的设计者希望通过严厉的惩罚来剔除作恶者，但在上述场景里，要追溯问题源头或定位恶意节点都是不可能的，严厉的惩罚是风险很高的。

拜占庭的故事构造的如此成功，区块链开发者无人不知。Lamport尝到了甜头，后来在《The Part-time Parliament》的论文中又讲了一个虚构的故事。这个故事发生在古希腊一个名叫Paxos的岛屿，作者将分布式一致性的问题比喻为岛上的立法机构如何对一项决议达成一致的问题。本来觉得用故事加以描述更易理解，但其结果完全相反，这篇文章的评审根本不吃这一套。当时的理论过于复杂，几乎没有人看懂，被埋没了多年，原文1998年才得以发表。后来Lamport又重新“正儿八经”地写了一篇《Paxos Made Simple》，似乎要做个简化版来照顾大家的智商。但这个题目和摘要真的害死人：

Abstract:
The Paxos algorithm, when presented in plain English, is very simple

论文的标题和摘要都说的很清楚了，简单啊！但作者其实十分恶意的讽刺了所有读者。我们引用另一篇文章中关于Paxos算法的描述，摘自USENIX ATC 2013的Best paper《In Search of an Understandable Consensus Algorithm》，大致含义说：Paxos真的太难懂了，很少有人不付出极大努力就能完全理解。在另一个高水平会议NSDI上，不少人对Paxos感到不爽。连点评者自己都和它做了很久的斗争，所以他这篇文章取名为“寻找一种易懂的一致性算法”...意思是还在寻找中，根本不像Lamport说的那么简单。后人无不感到Lamport深深的恶意，我们且来看看这个Paxos岛上到底发生了什么：

公元 10 世纪初，爱琴海上的小岛Paxos是一个兴盛的商业贸易中心。经济发展带来了政治的进步，Paxos 的公民们用议会形式的政府取代了原先的神权统治。议会的主要作用在于确定律法以保证城市可以有序稳定运转。所有律法都必须经由议会成员投票表决后方可生效实施，且已通过的律法必须被记录在案。但是对 Paxos人来说，做生意才是头等大事，城市职责反在其次，没有人愿意把他全部的时间投入到议会事务中。所以 Paxos 的议会必须在每个议员都可能随时缺席的情况下也能工作下去，这就是所谓的“兼职议会”。

一个现代的议会可以雇佣秘书来记录它的每一次活动和决议，但是在Paxos，没有一个人愿意始终呆在议会大厅里作为一个秘书从头到尾参与所有会议。取而代之的是每一个议员都会维护一个律簿，用来记录一系列已通过的法令，每个法令带有一个唯一编号。比如法令115要求工人按照15%费率缴个人所得税，法令135要求买东西也要交5%消费税...等等。如何保证议员手里的法令是最新的，又如何保证各个兼职议员手里的法令不冲突？了解比特币的朋友会觉得这个问题特别熟悉，没错，拜占庭和Paxos的故事都和区块链有关系，但分布式账本的概念其实和Paxos议会律簿更加接近。要完整解决去中心化的问题，不但要解决恶意节点，还需要能够运行在一个非常不稳定的兼职议会上。中本村结合前人的积累，创新的加入了“议会激励机制”，完成最后一脚。这种方法里的数学是如此“简单”，我们就不在这里赘述了，后面会继续通过一些小故事让大家理解。其实除了区块链，BFT容错还是很多航空航天信息系统的设计原则，是真正的火箭科技(Rocket Science)。

区块链中的数学